1. Космические скорости. Наиболее простой случай движения тел вблизи поверхности Земли под действием силы тяжести — свободное падение с начальной скоростью, равной нулю. В этом случае тело движется прямолинейно с ускорением свободного падения по направлению к центру Земли. Если тело имеет начальную скорость, величина которой отлична от нуля, и её вектор направлен не по вертикали, то тело под действием силы тяжести начнёт двигаться с ускорением свободного падения по криволинейной траектории.
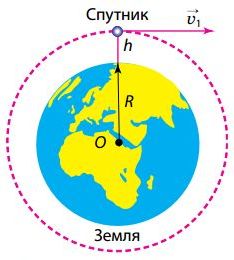
Рисунок 45 — Движение спутника по круговой орбите
Рассмотрим тело, находящееся за пределами земной атмосферы. Предположим, что вектор начальной скорости этого тела направлен по касательной к поверхности Земли. В зависимости от значения начальной скорости дальнейшее движение тела может быть различным:
- при малых начальных скоростях (u01, u02, u03) тело упадёт на Землю;
- при некотором определённом значении скорости u1 (первая космическая скорость) тело станет искусственным спутником и начнёт обращаться вокруг Земли подобно её естественному спутнику — Луне;
- при ещё большем увеличении значения скорости и достижении следующего определённого значения u2 (вторая космическая скорость) тело уйдёт от Земли так далеко, что сила земного притяжения практически не будет влиять на его движение. Тело начнёт обращаться вокруг Солнца подобно искусственной планете;
- наконец, если скорость тела достигнет определённого значения u3 (третья космическая скорость), то данное тело навсегда уйдёт из Солнечной системы в пространство Галактики.
Рассмотрим случай, когда тело становится искусственным спутником Земли, т. е. определим первую космическую скорость u1. Найдём эту скорость по второму закону Ньютона из условия, что под действием силы тяготения тело приобретает центростремительное ускорение: \[ G\frac{mM}{R_{орб}^2}=ma_ц, \] где Rорб = R + h — средний радиус орбиты тела (рис. 45), R — радиус Земли, h — высота тела над поверхностью Земли, М — масса Земли, m — масса тела (спутника).
Для центростремительного ускорения Подставляя это выражение в формула (1), после сокращений получаем:
Для центростремительного ускорения\( а_ц=\frac{\upsilon_1^2}{R_{орб}}=\frac{\upsilon_1^2}{R+h}. \) Подставляя это выражение в формула (1), после сокращений получаем:
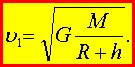
У поверхности Земли с учётом выражения для ускорения свободного падения
\( g=G\frac{M}{R^2} \)можно положить h = 0. Тогда первая космическая скорость (без учёта сопротивления воздуха) равна:
![]() Формула (2).
Формула (2).
Таким образом, тело, скорость которого равна 7,9 • 103 м/с и направлена по касательной относительно поверхности Земли, становится искусственным спутником Земли, движущимся по круговой орбите над Землёй. В небесной механике первая космическая скорость называется также круговой скоростью.
Вторая космическая скорость определяется из условия, что тело должно уйти из сферы земного тяготения и стать спутником Солнца. Расчёты дают следующее выражение для определения второй космической скорости (без учёта сопротивления воздуха): \( \upsilon_2=\sqrt{2gR} \) формула (3), где R — радиус Земли.
Используя выражение (2), находим:
![]() Подставляя в (4) уже известное нам значение первой космической скорости, получим, что у поверхности Земли v2 ≈ 11,2·103 м/с. Вторая космическая скорость называется также скоростью освобождения (убегания, ускользания) или параболической скоростью. Третья космическая скорость, или гиперболическая скорость, — это наименьшая начальная скорость, с которой тело должно преодолеть земное притяжение и выйти на околосолнечную орбиту со скоростью, необходимой для того, чтобы навсегда покинуть пределы Солнечной системы.
Подставляя в (4) уже известное нам значение первой космической скорости, получим, что у поверхности Земли v2 ≈ 11,2·103 м/с. Вторая космическая скорость называется также скоростью освобождения (убегания, ускользания) или параболической скоростью. Третья космическая скорость, или гиперболическая скорость, — это наименьшая начальная скорость, с которой тело должно преодолеть земное притяжение и выйти на околосолнечную орбиту со скоростью, необходимой для того, чтобы навсегда покинуть пределы Солнечной системы.
Расчёты дают следующую формулу для нахождения величины этой скорости: \( \upsilon_3=\sqrt{(\sqrt{2}-1)^2\upsilon^2+\upsilon_2^2} \) формула (5) где u » 29,8 • 103 м/с — скорость Земли на круговой орбите движения вокруг Солнца.
Подставляя значение второй космической скорости u2 в (5) и проведя расчёт, получим, что тело должно иметь минимальную скорость u3 » 16,7 • 103 м/с, чтобы покинуть пределы Солнечной системы.
2. Орбиты космических аппаратов. Расчёты траекторий полётов космических аппаратов связаны с использованием законов небесной механики. Следует заметить, что движение космических аппаратов описывается по законам небесной механики только после выключения реактивных двигателей. На пассивном участке траектории (т. е. после выключения двигателей) космические аппараты движутся под действием притяжения Земли и других тел Солнечной системы.
Элементы орбиты искусственных спутников Земли взаимосвязаны между собой формулой:
 формула (6) где u0 — начальная скорость спутника, M — масса Земли, r0 — расстояние точки выхода спутника на орбиту от центра Земли, a — большая полуось орбиты спутника.
формула (6) где u0 — начальная скорость спутника, M — масса Земли, r0 — расстояние точки выхода спутника на орбиту от центра Земли, a — большая полуось орбиты спутника.
Эксцентриситет орбиты е при горизонтальном запуске спутника равен
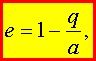 формула (7)
формула (7)
где q — расстояние перигея (ближайшей точки орбиты от центра Земли).

Рисунок 46 — Эллиптическая орбита искусственного спутника Земли
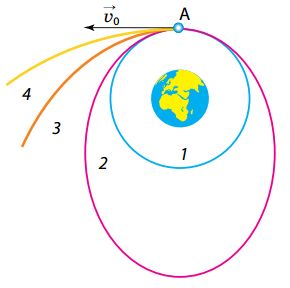
Рисунок 47 — Формы орбит космических аппаратов: 1 — круговая; 2 — эллиптическая; 3 — параболическая; 4 — гиперболическая
В случае эллиптической орбиты (рис. 46): q = a(1 – e) = R + hп, где hп — линейная высота перигея над поверхностью Земли. Расстояние апогея (наиболее удалённой точки орбиты от центра Земли): Q = a (1 + e) = R + hA, где hA — высота апогея над земной поверхностью, R — радиус Земли.
На рисунке 47 показаны орбиты космических аппаратов без учёта возмущений, т. е. когда аппараты остаются вблизи Земли. Но когда космический аппарат удалится от Земли на значительное расстояние, то на дальнейшее его движение будет оказывать влияние прежде всего притяжение Солнца. Радиус сферы действия Земли принимают равным примерно 930 тыс. км; на границе этой сферы влияние Солнца и Земли на космический аппарат одинаково. Момент достижения границы сферы действия Земли считается моментом выхода космического аппарата на орбиту относительно Солнца.
При запуске космических аппаратов к другим планетам исходят из следующих основных соображений:
- геоцентрическая скорость космического аппарата при выходе на орбиту относительно Земли должна превышать вторую космическую скорость;
- гелиоцентрическая орбита космического аппарата должна пересекаться с орбитой данной планеты;
- момент запуска необходимо выбрать так, чтобы орбита была наиболее оптимальной с точки зрения сроков полёта, затрат топлива и ряда других требований.
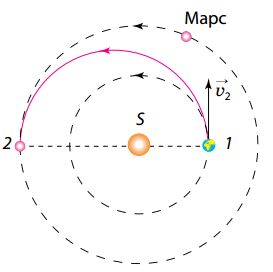
Одним из классов межпланетных траекторий являются энергетически оптимальные орбиты, которые соответствуют наименьшей геоцентрической скорости космических аппаратов в момент достижения границы сферы действия Земли. На рисунке 48 указана такая траектория перелёта на Марс, построенная на предположении, что орбиты Земли и Марса круговые. Данная орбита носит название гомановской, так как названа в честь немецкого астронома Вальтера Гомана, занимавшегося теорией межпланетных полётов.
В момент запуска космического аппарата Земля находится в точке 1. Гелиоцентрическая скорость v2 космического аппарата должна быть направлена так же, как и гелиоцентрическая скорость Земли, — по касательной к орбите Земли. Момент запуска следует подобрать так, чтобы космический аппарат и Марс, двигаясь по своим орбитам, достигли одновременно точки 2. Буквой S обозначено Солнце. Расчёты показывают, что время полёта с Земли до Марса по указанной траектории составит 259 суток (не считая сравнительно короткого времени полёта до границы сферы действия Земли).
3. Проблемы и перспективы космических исследований. Космонавтика — комплексная отрасль науки и техники, обеспечивающая исследование и использование космического пространства с помощью автоматических и пилотируемых космических аппаратов. Главными задачами космонавтики (в порядке их достижения) являются: вывод искусственного спутника на орбиту Земли, полёт человека в космос, полёт человека на Луну, полёт человека на другие планеты, полёт к звёздам. Первые три цели достигнуты.
Начало космической эры было положено в СССР запуском первого искусственного спутника Земли 4 октября 1957 г. Вторая важнейшая дата космической эры — 12 апреля 1961 г. В этот день Ю. А. Гагарин впервые в истории человечества совершил полёт в космос на космическом корабле «Восток». Третье историческое событие космонавтики — первая лунная экспедиция, осуществлённая 16—24 июля 1969 г. американскими астронавтами Н. Армстронгом, М. Коллинзом и Э. Олдрином. Значительный вклад в исследование космического пространства внесли и космонавты-белорусы П. И. Климук и В. В. Ковалёнок, О. В. Новицкий. Полёты человека в космос для нас стали уже почти обыденным явлением.
Современная теория космических полётов — астродинамика — основана на классической небесной механике и теории управления движением летательных аппаратов. Космонавтика нуждается в тщательной разработке оптимальных траекторий космических аппаратов с учётом ряда условий и ограничений.Космонавтика способствовала возникновению и развитию новых технологий. В перспективе — глобальный экологический мониторинг Земли, устранение угроз астероидно-кометной опасности.
Создание ракетно-космических комплексов — весьма сложная научно-техническая проблема. Космические аппараты должны обладать способностью к длительному самостоятельному функционированию в условиях космического пространства. Кроме того, возникает ряд дополнительных медико-биологических проблем (защита от космической среды, жизнеобеспечение экипажа и т. д.). Всё это требует разработки специальных систем. Для обеспечения полётов космических аппаратов необходима широкая сеть наземных служб управления.
По своей сущности космонавтика — это область общечеловеческой деятельности, и проводимая даже в рамках национальных проектов она затрагивает интересы многих стран.
Главные выводы
1. Скорость, при которой космический аппарат выводится на круговую орбиту вокруг небесного тела, называется первой космической скоростью.
2. Скорость, необходимая для того, чтобы космический аппарат вышел из сферы гравитационного действия Земли и обращался вокруг Солнца, называется второй космической скоростью.
3. Скорость, при которой космический аппарат, запущенный с Земли, покинет Солнечную систему, называется третьей космической скоростью.
4. Орбиты космических аппаратов представляют собой элементы эллипсов, парабол и гипербол.
Контрольные вопросы и задания
- Опишите первую, вторую и третью космические скорости.
- По каким орбитам могут двигаться космические аппараты? Каким геометрическим линиям соответствуют орбиты космических аппаратов для первой, второй и третьей космических скоростей?
- Какие орбиты космических аппаратов называют гомановскими?
- Определите период обращения искусственного спутника Земли, если наивысшая точка его орбиты над поверхностью Земли 36 тыс. км, а наинизшая — 300 км. Землю считать шаром радиусом 6370 км.
- Рассчитайте первую и вторую космические скорости для Луны. Учтите, что масса Луны — 7,35*1022 кг, а ее радиус — 1738 км.
- Искусственный спутник Земли запущен в плоскости земного экватора так, что все время находится в зените одной и той же точки земного шара. Определите высоту (h) этого ИСЗ над поверхностью Земли. При решении сравните движение спутника с движением Луны. ТЛ = 27,3 сут, аЛ = 384 000 км. Радиус Земли RЗ = 6400 км.
- Определите время полета космического аппарата от Земли до Марса по гомановской орбите. Большую полуось орбиты Марса принять равной 1,52 а. е.